ニュートン算には算数のもろもろが詰まっている

【問題】

牧草地に牛を放します。125頭の牛を放すと，8日間で牧草が食べつくされます。80頭の牛を放すと，13日間で牧草が食べつくされます。この牧草地で60頭の牛を放すと，何日間で牧草が食べつくされるかを答えなさい。
ただし，牛を放す前に生えている牧草地の草の量，毎日生える草の量はそれぞれ一定で，どちらも牛に食べられる前には枯れません。また，1頭の牛が毎日食べる草の量も一定とします。（北嶺中算数　2015平成27年改題）
　　 （元の出題は北海道の学校らしく1250頭で80日とか、牛も日数も多く、広いですね～）

問題のまとめ
●１２５頭の牛は８日間で草を食べつくす
●８０頭の牛なら１３日間で草を食べつくす
●６０頭なら何日で食べるか
●わかっていないのは何か。初めの草の量。毎日生える草の量。一頭の牛が毎日食べる草の量？これらは一定

【解法１　オーソドックスな線分図　これは仕事算？】

ポイント１、草の量の線分図。
　仕事算のようだが、全体量が決まってなさそうだ。イメージするため計算するための単位を考える。食べる草の量の単位はキログラムでもリットルでもよさそうだが、使いやすい単位を考える。
　そこで牛１頭が１日で食べる草の量を１草量とする。慣れたらただ「１」とおくが普通だが、この問題では勝手に１kg食べることに決めても解ける。
　（ニュートン算問題の中には数値が表記されているものもあり、比の問題のように①がいくらになるか検討する）


125頭が8日で食べ切った草の量は、
125頭×8日＝1000草量　（草は無くなったので、これは最初生えていた分と8日で生えた分の全部の量となる）
80頭が13日で食べた量は同じく　80頭×13日＝1040草量　（最初の分と13日で生えた分、牛が少ないので少し長持ちした、、、）
同じ草量なのに1000と1040と数字が違うのは、８日目以降も草が生えて来ているから。仕事算と同じような感じなのに、仕事が増えている！！
1040草量－1000草量＝40草量　この差の40草量は９日目から13日目までに生える草の量になる。
40草量÷(13－8）日＝8草量　一日で生える草の量が８草量（つまり、牛が8頭ならばちょうど最初と同じ草の量を維持できる。なのに125頭も飼うなんて不審だからここは計算間違いチェックポイントだな。）

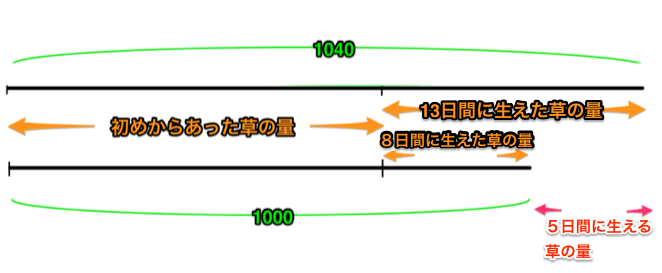
ポイント２、最初にあった量。
ここから逆算して、最初に生えていた草の量を出す。
8草量×8日＝64草量　これが8日であとから生えてきた草の量
４行目で計算した1000草が125頭が食べたすべての量だったから
1000草量－64草量＝936草量　これが初めの草の量
（13日で検算すると　8草量×13日＝104草量　1040－104＝936草量　間違いなし）

次のポイントは
「牛が60頭ならば、一日につき｛毎日60頭が60草量の草を食べるが、同時に毎日８草量だけ草は増えていくから｝
　60草量－8草量＝52草量づつ草の量が減ってゆく」 と考えるところだ。
最初生えていた936の草の量をを毎日52づつ減らしてゆくことになるから、
936草量÷52草量＝18日　　答え18日

まとめ
１、単位時間と単位処理力を決める。ここでは１草量。（指定のあるニュートン算もある。）
２、ケースごとの総仕事量は時間×処理力＋元からの量。二本の線分図を書く。
３、総仕事量の差は仕事増加量があるため
４、（処理能力ー増加量）が単位時間あたり仕事減少量で、元からの量からの減少割合を調べる。

【解法２　水量の変化にたとえる】

牛の頭数というのがニュートン算を難しくする原因で、実は頭数＝草を食べる量、仕事能力であったのだ。だから1頭が125頭分の草を食べても同じ（！）
そこで、下の図のように草を水に変えてみると水槽の問題になる。

牛の頭数（草を食べる量）＝水を減らす
生えてくる（増える）草＝増える水
毎日草が減る量は実際には（一日に食べる量－一日に生える量）となる。

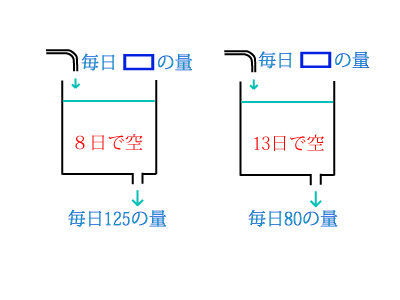解法１と異なり、１日の増減にも着目する。牛１頭が１日に食べる量を１とする。

80頭ならば一日80の草量ずつ食べ一日一定量生えるのでその差（80－１日に生える量）だけ最初の量から毎日減ってゆく
125頭ならば毎日（125－１日に生える量）だけ減らしてゆくことになる。

最初の草の量はどちらの場合も同じであり、ここから減ってゆき、最終的になくなる日数が8日だったり13日だったりとなる。
日数×毎日減らす量＝最初の草の量である。
13日×（80－1日に生える量）＝８日×（125－1日に生える量）＝最初の草の量

□を一日に生える草の量として
13×(80－□）＝8×(125－□)　　←この式に注目！ほかの解釈でも使う
1040－13×□＝1000－8×□
40＝５×□となり□＝８　つまり一日に生える草の量は８となる。

最初の草の量は、上の式の□に代入して
13×(80-8）＝936
60頭なら毎日60-8草を減らすから
936÷(60-8）＝18　答え18日

まとめ
１、単位時間の単位処理力を１と決める。
２、（処理能力ー増加量）が単位時間あたりの仕事減少量。
３、これを使って初期仕事量からの減少割合を比の式にする。仕事総量は不要。
または３、初期仕事量が一定、時間と仕事減少量が反比例している。

【解法３　旅人算のグラフ】

草の量に着目してグラフを書いてみると、下の図のようになる。
「食べる草」と「生える草」はそれぞれ速さだと考えられる。125頭だと毎日125の速さ、80頭だと毎日80の速さだ。毎時とか毎分と同じような「毎日」だ。
すこしづつ生えていく草の量に、牛がどんどん食べて迫っていき追いつく。距離が０になった時が、草の量が０になった地点だ。
これは最初の距離つまり草の量を、毎日（牛が食べるスピード125－草が生えるスピード○○）縮めていく追いつき旅人算である。計算は上の解法２と同様になる。また、グラフは解法１の図を縦置きにしたものでもある。
距離（初めの草の量）÷速さの差（125－□）＝時間８日
距離　　　　　　　　÷速さの差（80－□） ＝13日
13×(80－□）＝8×(125－□)　　　　←この式に注目！二回目の登場
以下、上の解法１や２と同じとなるので省略。
グラフを図形的に解く場合は80:125＝16:25として、13日目の縦の赤点線の長さが80の線と「ｘ軸」の作る三角形の相似比より16×13÷8＝26、８日目の縦の長さ25であるから、その差の１が40にあたることから、比の１あたり40、これが５日分だから生える草の速さ８、とでてくる。

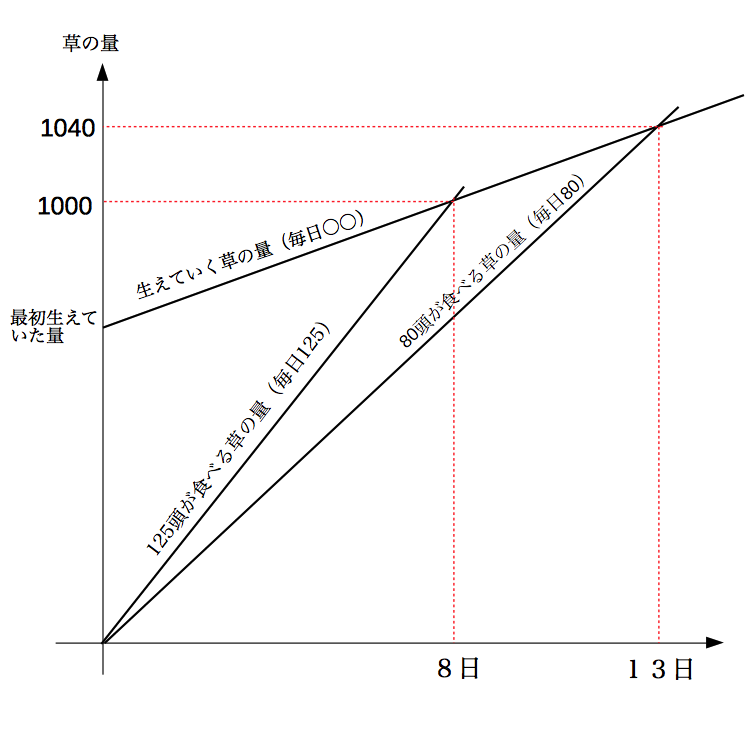
まとめ
１、処理能力と（総仕事＋増加量）はそれぞれが時間に比例しているのでケース毎のグラフを書く。
２、処理能力と総仕事量が一致した交点で仕事がゼロになる。

【解法3b　一次関数】

上のグラフを、中学生ならこう解く
ｙ＝80xにx=13を代入すると(13,1040)。ｙ＝125xにx=8を代入（8,1000)、 二点を通る直線はｙ＝8x＋936　（生えていく草の式） これとｙ＝60xとの交点よりx=18が求まる　

【解法３ｃまたは２ｂ　速さと比、距離の差】

　A君とBさんの現在位置ではなく二人の間のへだたりをグラフにした問題は少し高度な速さの問題です。
この問題では、解法３の上のグラフから、最初のへだたりを最初の草の量、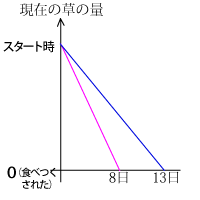隔たりがなくなれば０すなわち草の量も０と考え、右のグラフを作ります。単純なグラフです。
実はこれは、解法２の水槽の水の減り方をグラフ化したものです。
赤線が８日、青線が１３日なので、速さの比は逆比で赤：青＝１３：８
速さの比といっても、実は速さの差の比で、これは旅人算で、赤線が（125頭の速さー草の成長速度）、青線が（80ー成長速度）より
（125ー□）：（80ー□）＝１３：８　　←この式に注目！比だけど同じ式だ

【解法４　倍数算（年齢算）　相当算】

　「二人が同じ金額をもらったので最初の比と、後の比が変わった」という倍数算では、比を表のように書くのに慣れている人が多い。しかし、倍数算は比合わせでもあるので、線分図がわかりやすいように思われる。（だだし、線分を延長するような場合はまた別。）同じ金額をもらったので差は変わらない。親と子の年齢差が変わらない年齢算も倍数算のうち。

「毎日同じ量の草が生えてくる、比が変わる」差は一定。下の線分図参照。解法２同様一日当たりの増減に着目する。

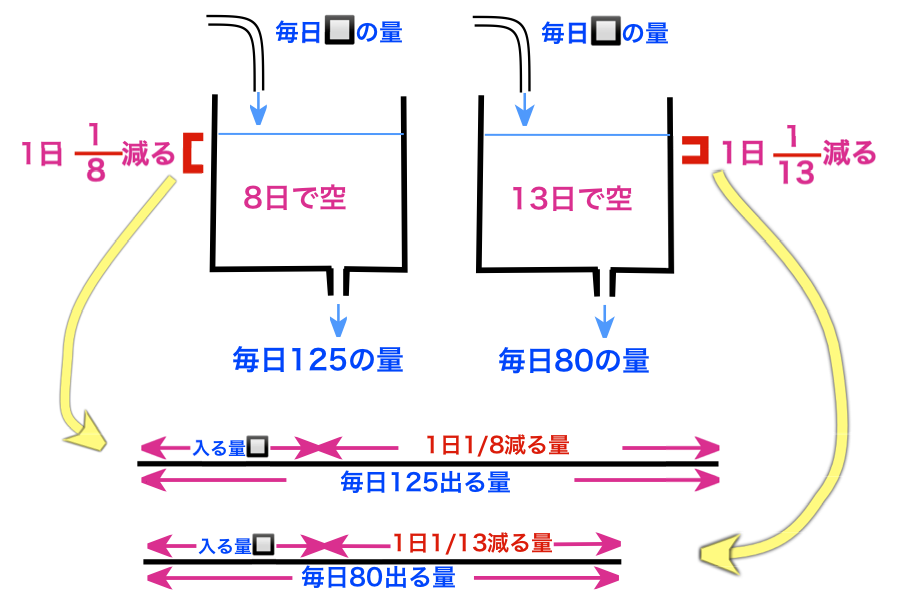
1日に食べる草は125頭分または80頭分で、それぞれ1日の仕事の量。1日に生えてくる草はどちらも同じ。その差が1日に減る量である。
（1日に食べる量−1日に生える量＝1日に減る量）

１３日で草がなくなるということは元あった草が一日に1/13減るということだし、８日でなくなるなら同じ元の草が毎日1/8減る。一日に減る量を比にする。　1/13：1/8＝８：13　逆比

一日当たり減る量の比　式A　　８：１３　　　比の差13-8=５
一日の仕事量（頭数）　式B　８０：１２５　　比の差125-80=45
下の線分図を見て比合わせをする。共通である比の差の数字５と45を同じ45にするために式Aを９倍する。倍数算の定石。
式A×９　　　　　　　式C　７２：１１７
式B－式C　は比の左も右も80－72＝125－117＝８
この８は倍数算の「共通にもらった金額＝一日で生える草」。式B、Cの比の数値は１が1頭だから、これは増える仕事つまり８頭分の草が1日に増えていることをあらわし、
また、比の差45は1日45頭分の仕事の差があるということ。

○内の数字は①につき９であるから、すべて９倍すれば数が合うようになる。
牛の例では、８頭分は生えてくる草を食べる仕事に割り当て、残りの117頭なり72頭なりが実質的な仕事に従事しているため、こちらが日数と逆比の関係にあるとも考えられる。

同じ式から次のようにする人もいるだろう。
式Bの比の１あたり45÷5＝９頭分の仕事 となる
13×9＝117　の仕事量　125ー117＝８

また、次の式を作って解く人もいるだろう。
125－生える草＝⑬
80－生える草＝⑧　として上の式を８倍、下の式を13倍する。
○104+⑧×生える草＝1000
○104+⑬×生える草＝1040
⑤＝40　より　①＝８
以下、⑧や⑬、⑤にあてはめる

まとめ
１、単位時間の単位処理力を１とおく
２、（処理能力ー増加量）が単位時間あたりの仕事減少量。
３、ケースごとの単位時間あたり仕事減少量の差の比の式を作り、比合わせ（倍数算）をする。

【解法５　逆比　反比例】

上の図の三本目の線を考える。もともと、水を減らす時間と減る水量は反比例している。仕事が２倍できれば（牛が2倍いれば）、かかる時間は１／２倍になる。

8日かかるのと13日かかるのでは、仕事の効率では1/8と1/13つまり13：8と逆比になる。
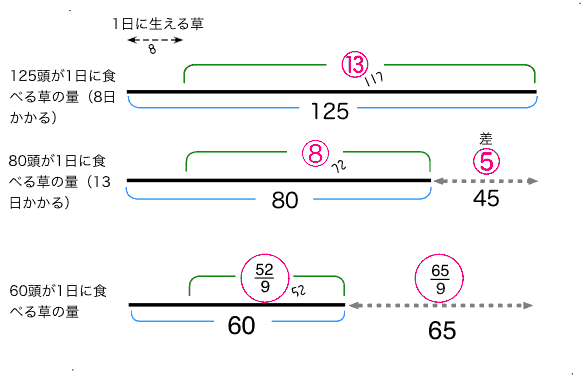
　反比例しているのは（食べる草ー生える草）の実質的な仕事であることに注意。解法2の水槽の図を思い出すと分かりやすい。一部の牛を生えてくる草専属と考えて除外してもよい。上の図では赤○つき数字が実質的仕事になる。一番上の線が8日間で草がなくなる場合、一日当たりの仕事は⑬。二本目は13日間でなくなる場合仕事は⑧。

三本目の線、60頭の場合が何日に当たるかこれから求める。
赤〇の比の値を求め、仕事と日数の反比例から答えを求める。分数になりそうだが、生えてくる草（＝8頭分）を求めなくても答えが出る。

牛の頭数が60に減ると仕事も125から60に減り少なくなった分が65（または80から20減ると考えてもよい）。①あたり９となるので、60頭の仕事は52／９に当たる。これが一定つまり日数と反比例するのだ。
反比例＝積が一定だから次の式ができる。
⑬×８日＝⑧×13日＝○52／9 × □日　　　←この式！実はずっと同じ式。
□＝18　　より答え18日

まとめ
１、単位時間の単位処理力を１とおく
２、（処理能力ー増加量）が単位時間あたりの仕事減少量。
３、初期仕事量は決まっているので、時間と仕事減少量が反比例している。

【解法７　方程式　消去算】

解法1が方程式にしやすい。

未知数として、初期の草をｙ、一日に生える草をｘとする。牛一頭が一日に食べる草を基準（１）とする。
ｙ＋８ｘ＝８×１２５
ｙ＋１３ｘ＝１３×８０
解法１はこれを消去算として解いたものでもある。また、ニュートン算では未知数を牛一頭が食べる量（一日の排出水量）に置くような問題もある。